杨辉三角形是排列成三角形的一系列数字。 在杨辉三角形中,每一行的最左边和最右边的数字总是 1。 对于其余的每个数字都是前一行中直接位于它上面的两个数字之和。
下面给出一个5行的杨辉三角:
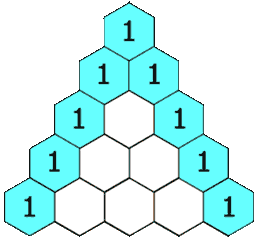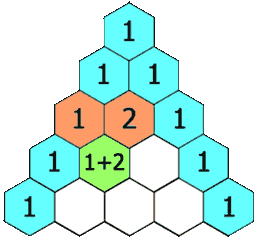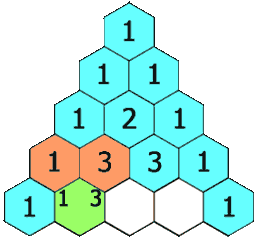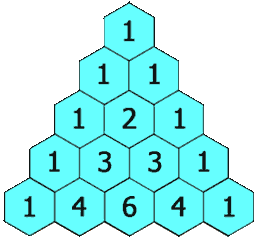
基本情况
可以看到,每行的最左边和最右边的数字是基本情况,在这个问题中,它总是等于 1。
因此,我们可以将基本情况定义如下:
f(i,j) = 1 where j=1 or j=i
递推关系
让我们从杨辉三角形内的递推关系开始。
首先,我们定义一个函数 f(i, j)它将会返回杨辉三角形第 i 行、第 j 列的数字。
我们可以用下面的公式来表示这一递推关系:
f(i,j)=f(i−1,j−1)+f(i−1,j)
java 实现
给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。
示例:
1
2
3
4
5
6
7
8
9
| 输入: 5
输出:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
|
方法一 迭代实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| public List<List<Integer> generateTrangle(int numRows){
List<List<Integer>> list = new ArrayList<>();
for(int i=0;i<numRows;i++){
List<Integer> subList = new ArrayList<>();
list.add(subList);
for(int j=0;j<i+1;j++){
f(j==i||j==0){
subList.add(1);
}else{
subList.add((list.get(i-1).get(j-1)+list.get(i-1).get(j)));
}
}
}
return list;
}
|
方法二 递归实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| public List<List<Integer>> generateTriangleByRecursive(int numRow) {
List<List<Integer>> list = new ArrayList<>();
for (int i = 0; i < numRow; i++) {
List<Integer> subList = new ArrayList<>();
for (int j = 0; j < i + 1; j++) {
subList.add(generate_Triangle_by_recursive(i, j));
}
list.add(subList);
}
return list;
}
private int generate_Triangle_by_recursive(int i, int j) {
int result;
if (j == 0 || j == i) {
result = 1;
} else {
result =
(generate_Triangle_by_recursive(i - 1, j - 1) + generate_Triangle_by_recursive(
i - 1, j));
}
return result;
}
|
在上面的例子中,您可能已经注意到递归解决方案可能会导致一些重复的计算,例如,我们重复计算相同的中间数以获得最后一行中的数字。 举例说明,为了得到 f(5, 3) 的结果,我们在 f(4, 2) 和 f(4, 3) 的调用中计算了 f(3, 2) 两次。下面我们优化递归算法
方法三 递归+记忆化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| public List<List<Integer>> generateTriangleByRecursive(int numRow) {
List<List<Integer>> list = new ArrayList<>();
Map<Integer, Map<Integer, Integer>> cacheMap = new HashMap<>();
for (int i = 0; i < numRow; i++) {
List<Integer> subList = new ArrayList<>();
for (int j = 0; j < i + 1; j++) {
subList.add(generate_Triangle_by_recursive(i, j, cacheMap));
}
list.add(subList);
}
return list;
}
private int generate_Triangle_by_recursive(int i, int j,
Map<Integer, Map<Integer, Integer>> cacheMap) {
if (cacheMap.containsKey(i) && cacheMap.get(i).containsKey(j)) {
return cacheMap.get(i).get(j);
}
int result;
if (j == 0 || j == i) {
result = 1;
} else {
result =
(generate_Triangle_by_recursive(i - 1, j - 1, cacheMap) + generate_Triangle_by_recursive(
i - 1, j, cacheMap));
}
if (!cacheMap.containsKey(i)) {
Map<Integer, Integer> map = new HashMap<>();
cacheMap.put(i, map);
}
cacheMap.get(i).put(j, result);
return result;
}
|
拓展算法
给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。
示例:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public List<Integer> getRow(int rowIndex) {
List<List<Integer>> list = new ArrayList<>();
for(int i=0;i<rowIndex+1;i++){
List<Integer> subList = new ArrayList<>();
list.add(subList);
for(int j=0;j<i+1;j++){
if(j==i||j==0){
subList.add(1);
}else{
subList.add((list.get(i-1).get(j-1)+list.get(i-1).get(j)));
}
}
}
return list.get(rowIndex);
}
|



